2. How to forecast sample size
Shigeru ONO
2024-05-22
vignette_size.Rmdここでは、rSurveyAssignパッケージを使った標本サイズ推定について
説明します。
rSurveyAssignパッケージの背後にある考え方については、 “rSurveyAssign: tools for simulation of assignment
in web surveys”を参照して下さい。
1. 標本サイズ推定の方法
このパッケージでは、以下の方法によって、調査に必要な対象者数を調べます。
- 架空の母集団データを用意します。
- 母集団データから対象者を復元抽出し、指定した方法でカテゴリ・スロットへの割付を行い、各スロットに割り付けられた対象者数が目標対象者数に到達したら終了します。これを割付試行と呼びます。
- 割付試行を十分な回数繰り返し、各試行において必要であった対象者数の分布を調べます。
2. データの準備
2.1 母集団データ
まず、母集団を表現するデータを用意します。
このデータは、母集団を有限集団として近似的に表現するものです。母集団メンバーそれぞれ について、カテゴリ・スロットへの割付可能性を記述します。
現バージョンのrSurveyAssignパッケージは、母集団データをつくる機能は提供していません。
過去の調査結果や既存の知識に基づき、なんとかして作ってください。
以下では、母集団メンバーを\(i (=1,\ldots,I)\), カテゴリを\(j(=1,\ldots,J)\), カテゴリ\(j\)のスロットを\(k (=1,\ldots,K_j)\)と表記します。
データのサイズ(\(I, J, K_1,...,K_J\))に制限はありません。母集団のメンバー数 \(I\) はできるだけ大きくしたほうがよいでしょう。
母集団データの例としてpopdataが用意されています。
popdataは、サイズ10000の有限集団のデータを持つデータフレームで、
カテゴリ数は3, スロット数は 各カテゴリについて10です(すなわち、\(I=10000, J=3, K_1=K_2=K_3=10\))。
内容をみてみましょう。
library(rSurveyAssign)
data(popdata, package = "rSurveyAssign")
head(popdata)
#> nID bCat_1 bCat_2 bCat_3 bSlot_1_1 bSlot_1_2 bSlot_1_3 bSlot_1_4 bSlot_1_5
#> 1 1 1 1 1 1 0 0 1 0
#> 2 2 1 1 1 1 1 1 1 0
#> 3 3 1 1 1 0 0 0 0 0
#> 4 4 0 0 0 NA NA NA NA NA
#> 5 5 1 1 1 0 0 0 0 0
#> 6 6 1 1 1 0 0 0 0 0
#> bSlot_1_6 bSlot_1_7 bSlot_1_8 bSlot_1_9 bSlot_1_10 bSlot_2_1 bSlot_2_2
#> 1 0 0 1 1 1 1 1
#> 2 0 0 0 1 0 1 0
#> 3 0 0 0 0 0 0 0
#> 4 NA NA NA NA NA NA NA
#> 5 1 0 0 0 0 0 0
#> 6 0 0 0 0 0 0 0
#> bSlot_2_3 bSlot_2_4 bSlot_2_5 bSlot_2_6 bSlot_2_7 bSlot_2_8 bSlot_2_9
#> 1 0 0 0 0 0 0 0
#> 2 1 0 1 0 0 0 0
#> 3 0 0 0 0 0 0 0
#> 4 NA NA NA NA NA NA NA
#> 5 0 0 0 0 0 0 0
#> 6 0 0 0 0 0 0 0
#> bSlot_2_10 bSlot_3_1 bSlot_3_2 bSlot_3_3 bSlot_3_4 bSlot_3_5 bSlot_3_6
#> 1 0 1 0 0 0 1 0
#> 2 0 0 0 0 0 0 0
#> 3 0 0 0 0 0 0 0
#> 4 NA NA NA NA NA NA NA
#> 5 0 0 0 0 0 0 0
#> 6 0 0 0 0 0 0 0
#> bSlot_3_7 bSlot_3_8 bSlot_3_9 bSlot_3_10
#> 1 0 0 1 0
#> 2 0 0 0 0
#> 3 0 0 0 0
#> 4 NA NA NA NA
#> 5 0 0 0 0
#> 6 0 0 0 0行は母集団のメンバーを表しています。
変数bCat_(i)は、カテゴリ\(i\)への割付可能性を表しています。
たとえば母集団メンバー1は、カテゴリ1,2,3に割付可能です。母集団メンバー4は、どのカテゴリにも割付不能です。
変数bSlot_(i)_(j)は、カテゴリ\(i\)のスロット\(j\)の割付可能性を表しています。
たとえば母集団メンバー1は、カテゴリ1のスロットのうち、スロット1, 4, 8,
9, 20に対して 割付可能です。
2.2 popdataオブジェクトの生成
次に、母集団データをrSurveyAssignパッケージが扱える形式に変換します。
rSurveyAssignパッケージは、母集団データを表すクラスpopdataを用意しています。
popdataクラスのオブジェクトは、関数makePopで作成します。
関数makePopの引数は次の2つです。
-
mbCAT: カテゴリ割付可能性。- \(I\)行\(J\)列の整数行列。
- \(i\)行\(j\)列の値は、「母集団メンバー\(i\)にとってカテゴリ\(j\)は割付可能か」 を表し、\(0\)は割付不能, \(1\)は割付可能を表します。
- 欠損は許容されません。
-
lSLOT: スロット割付可能性。- \(J\)個の要素からなるリスト。\(j\)番目の要素は、\(I\)行\(K_j\)列の整数行列。
- 要素\(j\)の行列の\(i\)行\(k\)列の値は、「母集団メンバー\(i\)にとって カテゴリ\(j\)のスロット\(k\)は割付可能か」を表し、\(0\)は割付不能, \(1\)は割付可能を表します。
-
mbCAT[i,j] == 1のとき、lSLOT[[j]][i,]}の欠損は許容されません。 すなわち、割付可能カテゴリに属するスロットの割付可能性は指定する必要があります。 -
mbCAT[i,j] == 0のとき、lSLOT[[j]][i,]は無視されます。すなわち、割付不能カテゴリに属するスロットの割付可能性は無視されます。従って欠損も許容されます。
では、データ例をpopdataクラスのオブジェクトに変換しましょう。
mbCat <- as.matrix(popdata[, paste0("bCat_", 1:3)])
lSlot <- list(
as.matrix(popdata[, paste0("bSlot_1_", 1:10)]),
as.matrix(popdata[, paste0("bSlot_2_", 1:10)]),
as.matrix(popdata[, paste0("bSlot_3_", 1:10)])
)
lPop <- makePop(mbCAT = mbCat, lSLOT = lSlot)
#> [makePop] assign colnames to lSLOT ...
#> [makePop] # of categories: 3
#> [makePop] # of slots: 10,10,10
#> [makePop] # of members: 10000
#> [makePop] # of member-category pairs which are assignable: 26488 (8829.3/category)
#> [makePop] # of member-slot pairs which are assignable: 58836 (1961.2/slot)無事に変換できました。
2. セッティング
次に、割付のセッティングを指定します。 詳細は“How to assign subjects”を参照してください。
- すべてのカテゴリのすべてのスロットに、すくなくとも10人の対象者を割り付けることにします。
- 回答負荷の観点から、ひとりの対象者が割り付けられるカテゴリは2つまで、スロットは2つまでとします。
- カテゴリの割付方法として
assignable-openclosed-open-none(ver 0.3までの指定方法ではadaptive,open,random,none)を使用します。 - スロットの割付方法として
assignable-shortnum-assignable-allclosed(ver 0.3までの指定方法ではadaptive,all,shortnum,allclosed)を使用します。 - すべてのスロットにおいて割り付けられた対象者数が目標に到達したときに調査を停止します。
lSetting <- makeSetting(
lSLOT_REQUEST = lapply(lSlot, function(mbSlot) rep(10, ncol(mbSlot))),
nCAT_MAX = 2,
nSLOT_MAX = 2,
sCAT_ASSIGN = 'assignable-openclosed-open-none',
sSLOT_ASSIGN = 'assignable-shortnum-assignable-allclosed',
bSTOP_WHEN_FULFILLED = TRUE
)
#> [makeSetting] assign names to lSLOT_REQUEST ...3. 割付シミュレーション
では、必要な標本サイズを推定するために、シミュレーションを行ってみましょう。
3.1 単一の試行の実行
まず、割付試行を1回行ってみます。
set.seed(123) # 結果を再現するために乱数のシードを設定している。通常は設定不要
dfResult <- simSize (
lPOP = lPop, # データを指定する
lSETTING = lSetting # セッティングを指定する
)
#> [execTrials] start trials (serial) ...
#> [execTrials] nTrial: 1 ; extract: 459 ; 0.056 sec.
#> [execTrials] end trials.コンソールに表示されるメッセージは、各試行の結果を表しています。この試行では、母集団から調査対象者を459人抽出したところで 調査が終了しました。
シミュレーションの結果をみてみましょう。
head(dfResult)
#> # A tibble: 6 × 9
#> sRowname nPerson nCat1 nCat2 nParentCat nSlot1 nSlot2 nTrial nSubject
#> <chr> <int> <int> <int> <int> <int> <int> <int> <int>
#> 1 1 6779 1 2 1 9 6 1 1
#> 2 2 5953 2 3 3 10 9 1 2
#> 3 3 3232 3 1 NA NA NA 1 3
#> 4 4 1226 3 2 3 2 5 1 4
#> 5 5 5372 1 NA 1 7 10 1 5
#> 6 6 7652 2 1 2 2 1 1 6このシミュレーションでは、1人目の調査対象者として母集団メンバー6779が抽出されました。カテゴリ割付の結果、カテゴリ1,2が割り付けられました。スロット割付の結果、カテゴリ1のスロット6,9が割り付けられました。
このシミュレーションで、各スロットには何人の対象者が割り付けられたのでしょうか? 調べてみましょう。
mnIn <- rbind(
as.matrix(dfResult[c("nParentCat", "nSlot1")]),
as.matrix(dfResult[c("nParentCat", "nSlot2")])
)
table(mnIn[,1], mnIn[,2])
#>
#> 1 2 3 4 5 6 7 8 9 10
#> 1 11 11 12 11 10 11 11 11 12 12
#> 2 13 13 13 10 13 13 10 14 10 10
#> 3 10 11 11 11 11 10 12 10 13 10上の表は、行がカテゴリ、列がスロット、値がそのスロットに割り付けられた人数を表しています。すべてのスロットに10人以上が割り付けられていることを確認できます。
3.2 多くの試行の実行と保存
上の例では、割付試行を1回行い、 シミュレーションの結果をデータフレームとして取得しました。
標本サイズを推定するには、十分な数の割付試行を繰り返す必要があります。 そこで今度は、割付試行を500試行繰り返してみましょう。
シミュレーションの結果はサイズが大きいので、いったんSQLiteデータベース上に
保存したほうがよいでしょう。 以下の例では、
SQLiteデータベースファイルとして、../tools/rSurveyAssign_vignette_size_1.sqliteを
作成します。実際には、適切なフォルダとファイル名を指定してください。また、
データベースファイルは必要がなくなったら自分で消してください。
実行時間を短くするため、並列処理を行うことにします。引数bPARALLELにTRUEを指定します。
並列処理を行う場合、各試行についてのメッセージは画面に表示されません。
そこでログファイルを作成することにします。
実行に長い時間がかかる場合は、ログファイルを監視すると、
いま何試行まで進んでいるかわかり、少しだけ心が癒されるでしょう。
下の例では、ログファイルをC:/work/simSize.logとしています。
RStudioを使っているなら、Terminalウィンドウでtail -F C:/work/simSize.logを
実行すると、ログファイルを監視できます。
## 都合によりコメントアウトしています
# set.seed(123) # 結果を再現するために乱数のシードを設定している。通常は設定不要
# dfResult <- simSize (
# lPOP = lPop,
# lSETTING = lSetting,
# nNUMTRIAL = 500,
# bPARALLEL = TRUE,
# sLOGFILE = "c:/work/simSize.log",
# sDBPATH = "../tools/rSurveyAssign_vignette_size_1.sqlite",
# bAPPEND = FALSE # すでにデータベースが存在する場合は上書きする
# )関数getSize_rawで、
データベースに格納された結果をそのまま取り出すことができます。
head(getSize_raw("../tools/rSurveyAssign_vignette_size_1.sqlite", nTRIAL = 1))
#> # A tibble: 6 × 9
#> sRowname nPerson nCat1 nCat2 nParentCat nSlot1 nSlot2 nTrial nSubject
#> <chr> <int> <int> <int> <int> <int> <int> <int> <int>
#> 1 1 8470 2 3 2 1 2 1 1
#> 2 2 9210 1 2 1 10 7 1 2
#> 3 3 5801 2 1 2 1 NA 1 3
#> 4 4 6816 3 2 3 7 9 1 4
#> 5 5 4868 NA NA NA NA NA 1 5
#> 6 6 688 1 2 1 2 3 1 6なお、これまでにデータベースに格納した試行数は、格納した際に表示されますが、
関数countSizeで調べることもできます。
countSize("../tools/rSurveyAssign_vignette_size_1.sqlite")
#> [1] 500この例では、500試行の実行に数秒しかかかりませんが、
もっと長い時間がかかることもあるでしょう。そうした場合に、
試行数nNUMTRIALを大きくすると、
simSizeの実行にとても長い時間がかかることになり、不便です。
このような場合は、nNUMTRIALはあまり時間がかからない程度の大きさにとどめ、
simSizeを気が向いたときに繰り返し実行して、結果を少しずつデータベースに
蓄積していくのが良いでしょう。
その際は、初回実行時には引数bAPPENDをFALSEとし、
二回目以降の実行時にはTRUEとしてください。また、引数lPOP,
lSETTINGに与える値を途中で変えないように注意して下さい(少しでも変えるとエラーとなります)。
4. 標本サイズの推定
データベースに格納されている試行結果を集計して取り出すためには、
関数getSizeを使います。
4.1 調査対象者数
関数getSizeの引数sTYPEをsubjectとすると、
各試行における調査対象者数を調べることができます。
dfResult_s <- getSize (
sTYPE = "subject",
sDBPATH = "../tools/rSurveyAssign_vignette_size_1.sqlite"
)
print(dfResult_s)
#> # A tibble: 500 × 3
#> nTrial nNum_scr nNum_main
#> <int> <int> <int>
#> 1 1 420 189
#> 2 2 504 192
#> 3 3 480 181
#> 4 4 459 179
#> 5 5 365 186
#> 6 6 568 189
#> 7 7 679 187
#> 8 8 425 187
#> 9 9 705 195
#> 10 10 529 192
#> # ℹ 490 more rowsnNum_scrは調査対象者数,
nNum_mainはそのうち1つ以上のスロットに割り付けられた人数を表しています。
調査対象者数の平均を求めてみましょう。
必要な調査対象者数の平均は約522人となりました。
実務的には、必要な調査対象者数の平均だけではなく、その分散にも関心が持たれます。 仮に分散が大きい場合、実際に調査を行った際の調査対象者数は運悪く大きな値となり、 予算をオーバーしてしまいかねません。 そこで、500回の試行を通じた調査対象者数の分布を調べてみましょう。
g <- ggplot2::ggplot(data = dfResult_s, ggplot2::aes(x = nNum_scr))
g <- g + ggplot2::geom_histogram()
g <- g + ggplot2::theme_bw()
print(g)
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.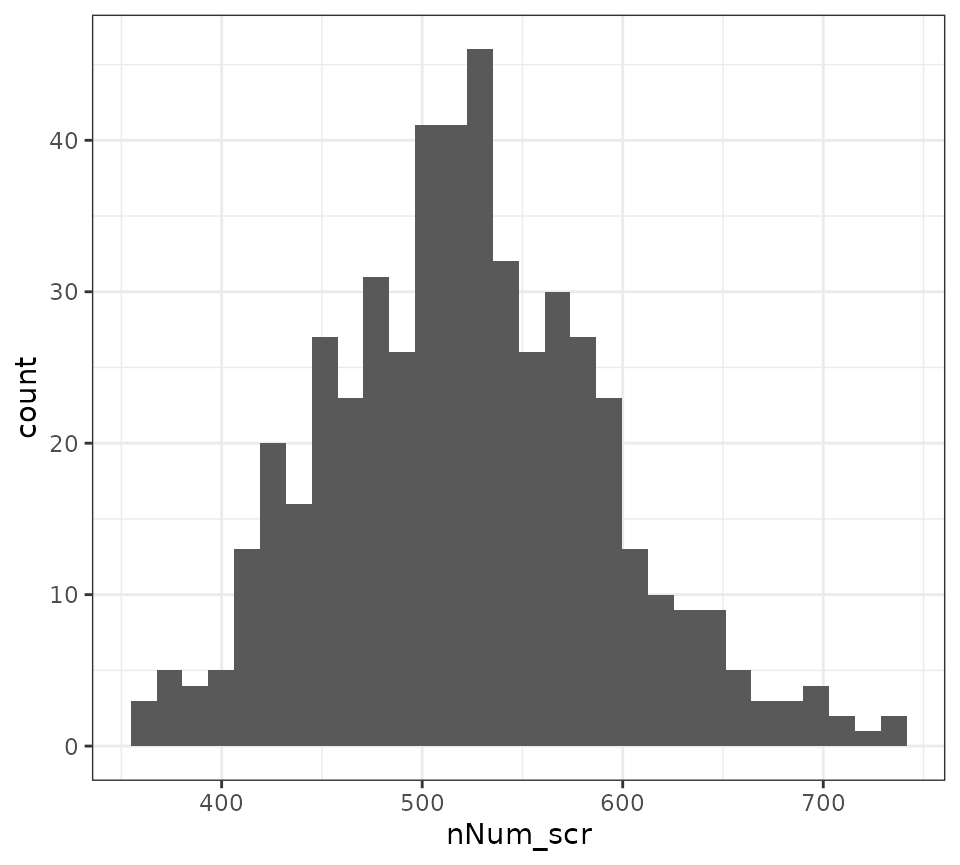
たいていの場合は600人程度で終了しますが、たまにはそれを超えてしまうこともあるようです。
4.2 カテゴリ・スロットあたり調査対象者数
関数getSizeの引数sTYPEをcatとすると、各カテゴリの割付人数を調べることができます。
dfResult_c <- getSize (
sTYPE = "cat",
sDBPATH = "../tools/rSurveyAssign_vignette_size_1.sqlite"
)
print(tapply(dfResult_c$nNum, dfResult_c$nCat, mean))
#> 1 2 3
#> 317.416 350.768 245.866カテゴリ1, 2, 3の割付人数は、平均してそれぞれ約318人, 350人, 245人となりました。
関数getSizeの引数sTYPEをslotとすると、各スロットの割付人数を調べることができます。
dfResult_s <- getSize (
sTYPE = "slot",
sDBPATH = "../tools/rSurveyAssign_vignette_size_1.sqlite"
)
print(tapply(dfResult_s$nNum, list(dfResult_s$nParentCat, dfResult_s$nSlot), mean))
#> 1 2 3 4 5 6 7 8 9 10
#> 1 11.580 11.074 11.240 11.294 10.002 11.194 10.890 11.144 11.690 12.522
#> 2 13.532 12.910 12.608 10.220 12.918 12.234 10.378 12.988 10.452 11.154
#> 3 11.328 10.902 11.150 11.034 11.096 10.000 11.196 11.080 11.310 10.822たとえば、カテゴリ1のスロット1の割付人数は、平均して約11.5人となりました。
割付人数が目標である10人を超えるのは、この割り付け方法の場合、 すでに目標に到達しているスロットへの割付が発生する場合があるからです。
5. 分析例: 割付方法の比較
調査に必要な対象者数がカテゴリ割付・スロット割付の方法によって どのように変わるかを、シミュレーションによって推測することができます。
たとえば、スロット割付の方法をassignable-random-assignable-allclosed
(ver
0.3までの指定方法ではadaptive,all,random,allclosed)に変更して
シミュレーションしてみます。
SQLiteデータベースファイルとして、../tools/rSurveyAssign_demo2.sqliteを
作成します。20試行実行します。
lSetting2 <- makeSetting(
lSLOT_REQUEST = lapply(lSlot, function(mbSlot) rep(10, ncol(mbSlot))),
nCAT_MAX = 2,
sCAT_ASSIGN = 'assignable-openclosed-open-none',
nSLOT_MAX = 2,
sSLOT_ASSIGN = 'assignable-random-assignable-allclosed',
)
#> [makeSetting] assign names to lSLOT_REQUEST ...
set.seed(1234) # 結果を再現するために乱数のシードを設定している。通常は設定不要
simSize (
lPOP = lPop,
lSETTING = lSetting2,
nNUMTRIAL = 20,
sDBPATH = "../tools/rSurveyAssign_vignette_size_2.sqlite",
bAPPEND = FALSE
)
#> [execTrials] start trials (serial) ...
#> [execTrials] nTrial: 1 ; extract: 1235 ; 0.093 sec.
#> [execTrials] nTrial: 2 ; extract: 1021 ; 0.084 sec.
#> [execTrials] nTrial: 3 ; extract: 1206 ; 0.096 sec.
#> [execTrials] nTrial: 4 ; extract: 1398 ; 0.104 sec.
#> [execTrials] nTrial: 5 ; extract: 1156 ; 0.093 sec.
#> [execTrials] nTrial: 6 ; extract: 931 ; 0.074 sec.
#> [execTrials] nTrial: 7 ; extract: 1682 ; 0.125 sec.
#> [execTrials] nTrial: 8 ; extract: 1640 ; 0.128 sec.
#> [execTrials] nTrial: 9 ; extract: 1516 ; 0.109 sec.
#> [execTrials] nTrial: 10 ; extract: 1293 ; 0.196 sec.
#> [execTrials] nTrial: 11 ; extract: 966 ; 0.072 sec.
#> [execTrials] nTrial: 12 ; extract: 1023 ; 0.078 sec.
#> [execTrials] nTrial: 13 ; extract: 1515 ; 0.11 sec.
#> [execTrials] nTrial: 14 ; extract: 931 ; 0.074 sec.
#> [execTrials] nTrial: 15 ; extract: 1518 ; 0.109 sec.
#> [execTrials] nTrial: 16 ; extract: 1393 ; 0.102 sec.
#> [execTrials] nTrial: 17 ; extract: 1150 ; 0.089 sec.
#> [execTrials] nTrial: 18 ; extract: 1585 ; 0.115 sec.
#> [execTrials] nTrial: 19 ; extract: 1239 ; 0.094 sec.
#> [execTrials] nTrial: 20 ; extract: 1359 ; 0.102 sec.
#> [execTrials] end trials.
#> [simSize] # Accumlated Trials: 20
#> NULL
dfResult2_s <- getSize (
sTYPE = "subject",
sDBPATH = "../tools/rSurveyAssign_vignette_size_2.sqlite"
)
print(mean(dfResult2_s$nNum_scr))
#> [1] 1287.85必要な調査対象者数の平均は約1287人となりました。
スロット割付方法をassignable-shortnum-assignable-allclosedとしたときの調査対象者数の平均は約522人でしたから、
こちらの割付方法のほうがはるかに多くの調査対象者を必要とすることがわかります。